GUÍA DE EXAMEN

EXAMEN UNIDAD 3

Propiedades de la igualdad

La igualdad relaciona dos expresiones con el signo “=”, la igualdad tiene algunas propiedades que son verdades evidentes, no requieren ser demostradas, a partir de estas propiedades se pueden demostrar otras propiedades. Las primeras cuatro propiedades que se muestran a continuación son propiedades evidentes de la igualdad:

Considera que a, b, c  R

Una ecuación es una igualdad matemática entre dos expresiones algebraicas que se relacionan a través de operaciones matemáticas y que contienen valores desconocidos llamados variables

Clasificación  de ecuaciones 

(ver página 111 del libro)

Ecuaciones lineales con una incógnita

Las ecuaciones lineales o de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.

Ejemplo:

Agrupamos los términos semejantes y los independientes, y sumamos:

Ecuaciones lineales con dos incógnitas

Una ecuación lineal con dos incógnitas es una igualdad algebraica del tipo: ax+by = c, donde x e y son las incógnitas, y a, b y c son números conocidos.

Una solución de una ecuación lineal con dos incógnitas es un par de valores (x,y) que hacen cierta la igualdad.

 Método de igualación:

 Método de sustitución:

Ecuaciones cuadráticas

Tipos: (Pag 138)

• Ecuaciones cuadráticas incompletas puras:

Ejemplo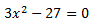 

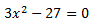
Despejamos x y hacemos la raíz cuadrada (no olvidemos el doble signo)

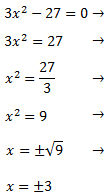
• Ecuaciones cuadráticas incompletas mixtas:

Factorizamos la expresión y nos queda un producto de x por una ecuación. Por tanto, el producto es 0 si x = 0 o la ecuación vale 0.

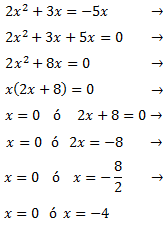
• Ecuaciones cuadráticas completas:

• Método de solución por fórmula general

ACTIVIDAD: 

1. DESCARGAR EL CUESTIONARIO UNIDAD 3,
2. IMPRIMIR Y CONTESTAR
3. ENTREGARLO EN VIGILANCIA EL MARTES 29 A LAS 7:00 HRS.